-
[프로그래머스] 등산코스 정하기(JavaScript)Problem-Solving/Problem 2022. 9. 7. 17:34
🍀 목차
문제
설계
구현(JavaScript)
최종 코드
훔쳐보기문제
https://school.programmers.co.kr/learn/courses/30/lessons/118669
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
설계
코딩 테스트에서 이 문제를 마주쳤을 때는 DFS로 접근했었는데, 테스트 케이스에서 틀리고 시간 복잡도도 엄청났던 코드였다.
몇 개월 뒤 다시 보니 시작 정점에서 목적 정점까지의 최소 거리를 구하는
다익스트라알고리즘으로 접근할 수 있는 문제라고 생각했다. 그러나 몇 시간 동안 헤맸지만 테스트 케이스 3개에서 계속 시간 초과가 발생했고, 결국 카카오 기술 블로그 해설을 참조하여 아이디어를 얻어 풀 수 있었다. 매일 쉬운 문제만 풀다가 호되게 혼난 느낌이다. 💀- 시간 초과가 발생했던 이유
- gates 배열을 for 문을 돌며 gate를 시작점으로 잡고 다익스트라를 매번 실행했다.
- 시간 초과를 개선한 설계
- 모든 gate를 시작점으로 넣고, 다익스트라는 한 번만 실행한다.
- 가지치기 1 : 현재 vertex에 기록된 intensity보다 MinHeap에서 나온 cost가 크다면 현재 기록된 intensity가 최소 intensity므로 하위 로직을 진행하지 않고 continue 해준다.
- 가지치기 2 : MinHeap에서 나온 vertex가 summits(산봉우리들) 중 하나라면 continue 해준다. (우리는 산봉우리 도착 후 다음의 로직을 보지 않는다. <부가적인 설계> 첫번째 list item을 확인. 👇)
- 부가적인 설계
- 1 - 2 - 3 - 2 - 1 의 등산코스에서 산봉우리가 3번이라고 할 때 👉 1 - 2 - 3 - 2 - 1 의 다시 돌아오는 코스는 굳이 생각하지 않아도 된다. (출입구에서 산봉우리까지의 최소 intensity를 찾았다면 돌아올 때도 온 길을 똑같이 돌아와야 할 것이다. intensity가 최소가 되는 값을 찾아야 하기 때문이다.)
- 2차원 인접 행렬을 만들기에는 n의 범위(최대 50,000)가 크다. 👉 인접 리스트를 만들자.
- 해당 정점이 산봉우리인지 파악할 때, 시간 복잡도를 줄이기 위해서는 Array.prototype.includes()보다는 다른 방법을 사용하는 것이 좋아 보인다. 👉 boolean 배열에 표시를 하는 건 어떨까?
- 들어올 수 있는 최대 intensity 값은 10,000,000이다. 👉 MAX_VALUE를 10,000,001로 생각해도 된다.
- intensity가 최소가 되는 등산코스가 여러 개라면 그중 산봉우리 번호가 가장 낮은 코스를 선택한다. 👉 미리 오름차순 정렬해주면 편할 것 같다.
다익스트라를 한 번만?
카카오 기술 블로그 해설을 보면 자세히 나와있지만, 대략적으로 요약하면.
다익스트라를 변형하여 distance 배열이 아닌, intensity를 기록하는 배열을 생성한다. 다익스트라를 진행시키며 intensity 배열을 갱신한다.
다음 정점에 기록된 최소 intensity보다 현재 정점의 최소 intensity와 다음 정점으로의 cost를 비교한 max값(3과 5가 있다면 5가 intensity가 되므로)이 더 작다면 intensity를 갱신한다. (처음 방문했거나 다른 곳을 거쳐서 오는 경우가 더 작은 경우)if intensity[nextVertex] > Math.max(intensity[vertex], nextCost) then intensity[nextVertex] = Math.max(intensity[vertex], nextCost)
결과적으로 우리가 필요한 것은 최소 intensity를 가지는 최소 산봉우리 번호이다. "몇번 출입구에서 시작했는지" 에 대한 정보는 필요 없다. 모든 출입구를 시작 정점으로 생각하여 minHeap에 넣고 다익스트라를 실행시키면 결국 모든 출입구에서 등산코스를 진행, 산봉우리들의 최소 intensity가 기록되어 있다.구현(JavaScript)
우선 paths를 연결 정보를 저장할 인접 리스트를 생성한다.
const hikingTrail = Array.from({length:n+1},()=> []); paths.forEach((path)=>{ const [i,j,w] = path; hikingTrail[i].push([j,w]); hikingTrail[j].push([i,w]); });
세팅이 다 된 후 이제 해당 정점이 산봉우리임을 표시하는 boolean 배열을 만들어준다.
const isSummits = Array.from({length:n+1},()=> false); summits.forEach((summit)=>{ isSummits[summit] = true; });그 외 부가적인 설계였던 MAX 설정, summits sort 등을 선언한다.
const MAX = 10000001; const answer = [n, MAX]; summits.sort((a,b)=> a-b);다익스트라에 사용할 MinHeap을 구현해준다. 구현 방법은 다익스트라 포스팅에서 사용했던 코드와 동일하다.
class Heap { constructor(){ this.items = []; } swap(idx1, idx2){ [this.items[idx1], this.items[idx2]] = [this.items[idx2], this.items[idx1]]; } findParentIdx(idx){ return Math.floor((idx-1)/2); } findLeftChildIdx(idx){ return idx*2+1; } findRightChildIdx(idx){ return idx*2+2; } findParent(idx){ return this.items[this.findParentIdx(idx)]; } findLeftChild(idx){ return this.items[this.findLeftChildIdx(idx)]; } findRightChild(idx){ return this.items[this.findRightChildIdx(idx)]; } size(){ return this.items.length; } } class MinHeap extends Heap{ bubbleUp(){ let index = this.items.length-1; while(this.findParent(index) && this.findParent(index)[1]>this.items[index][1]){ this.swap(index, this.findParentIdx(index)); index = this.findParentIdx(index); } } bubbleDown(){ let index =0; while((this.findLeftChild(index) && this.findLeftChild(index)[1] < this.items[index][1]) || (this.findRightChild(index) && this.findRightChild(index)[1] < this.items[index][1])){ let smallerIndex = this.findLeftChildIdx(index); if(this.findRightChild(index) && this.findRightChild(index)[1] < this.items[smallerIndex][1]){ smallerIndex = this.findRightChildIdx(index); } this.swap(index, smallerIndex); index = smallerIndex; } } add(value){ this.items.push(value); this.bubbleUp(); } poll(){ if(this.size() === 1){ return this.items.pop(); } const value = this.items[0]; this.items[0] = this.items.pop(); this.bubbleDown(); return value; } }다익스트라 알고리즘을 구현한다. 다익스트라 알고리즘이 끝나면, 기록된 intensity 배열을 리턴한다.
function dijkstra(){ const minHeap = new MinHeap(); const intensity = Array(n+1).fill(MAX); // 모든 출발지에서 시작해준다. gates.forEach((gate)=>{ minHeap.add([gate,0]); intensity[gate]=0; }); // ... return intensity; }모든 출입구를 시작 정점으로 생각하여 minHeap에 넣고 다익스트라를 실행해줘야 한 번의 다익스트라로 산봉우리들의 intensity를 구할 수 있다.

세팅이 다 된 후 이제 minHeap에서 cost가 작은 순대로 [vertex, cost] 형태로 꺼내 다익스트라를 수행할 것이다.
만약 vertex에 기록된 intensity보다 minHeap에서 나온 cost의 intensity가 크다면, 최소 intensity가 아니기 때문에 continue 해준다.
또한, 우리는 산봉우리에 도착한 다음의 등산코스를 더 진행하지 않기로 했기 때문에 vertex가 산봉우리라면 continue 해준다.
while(minHeap.size()){ const [vertex, cost] = minHeap.poll(); if(intensity[vertex] < cost){ continue; } if(isSummits[vertex]){ continue; } const adjList = hikingTrail[vertex]; const adjListLen = adjList.length; for(let i=0;i<adjListLen;i++){ const [nextVertex, nextCost] = adjList[i]; if(intensity[nextVertex] > Math.max(intensity[vertex], nextCost)){ intensity[nextVertex] = Math.max(intensity[vertex], nextCost); minHeap.add([nextVertex, intensity[nextVertex]]); } } }그림으로 과정을 이해해보자. minHeap에서 [vertex,cost] = [1,0]이 poll 되고, intensity[vertex] = 0, cost 0을 비교한다.
문제가 없기 때문에 넘기고, vertex 1은 산봉우리가 아니므로 등산코스를 진행한다.
연결정보를 기록했던 hikingTrail을 활용하여 1과 연결된 2 정점을 탐색한다.
상황은 아래 그림과 같다.

1 -> 2 [nextVertex, nextCost] = [2,3]이며 intensity[nextVertex]는 초기화에 의해 MAX가 기록되어 있다. intensity[1]과 nextCost인 3 중 더 큰 값이 1 -> 2로 가는 최소 intensity가 될 것이다.
그리고 이동 후에는 다음 등산코스 진행을 위해 minHeap에 넣어줘야 한다.
intensity[2] = MAX > Math.max(3,intensity[1]) = 3 이므로 갱신 후 minHeap에 넣어준다.

다음으로 minHeap에서 [vertex, cost] = [3,0]이 나오게 된다.

3 -> 2, 3 -> 4 현재 intensity[3]은 0이고 cost도 0이기에 진행, 3은 산봉우리가 아니기에 하위 로직 진행.
3과 연결된 정점 중 2와 4를 탐색.
① 2의 경우
[nextVertex, nextCost] = [2,5]
intensity[2] = 3과 Math.max(intensity[3], nextCost) = 5를 비교. 현재 기록된 nextVertex의 intensity가 더 최소이기 때문에 탐색을 종료한다.
② 4의 경우
[nextVertex, nextCost] = [4,4]
intensity[4] = MAX와 Math.max(intensity[3], nextCost) = 4를 비교.
nextVertex의 intensity를 최소 intensity로 갱신시킨다. 그리고 [4,4]를 minHeap에 넣어 다음 등산코스를 진행시킨다.

...(반복)
minHeap이 빌 때까지 다익스트라로 산봉우리들의 최소 intensity를 갱신시켜준다. 과정은 아래와 같다.
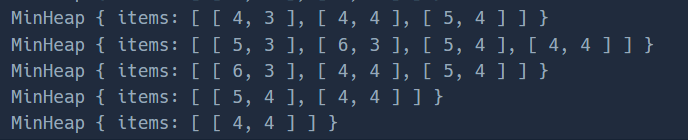
최종적으로 다익스트라 함수가 종료 후, 리턴된 intensity배열은 아래와 같다.

우리는 산봉우리들의 intensity만 보면 된다. 앞서 정렬을 시켜줬기에, 산봉우리 번호가 낮은 순대로 summits를 순회하며 산봉우리 번호와 그 값을 answer에 기록해주면 끝!
(정렬을 시켜주지 않아도 되지만, if-else문이 가독성이 떨어져 정렬을 해주었다!)
summits.forEach((summit) => { if (intensity[summit] < answer[1]) { answer[0] = summit; answer[1] = intensity[summit]; } }); return answer;최종 코드
class Heap { constructor() { this.items = []; } swap(idx1, idx2) { [this.items[idx1], this.items[idx2]] = [this.items[idx2], this.items[idx1]]; } findParentIdx(idx) { return Math.floor((idx - 1) / 2); } findLeftChildIdx(idx) { return idx * 2 + 1; } findRightChildIdx(idx) { return idx * 2 + 2; } findParent(idx) { return this.items[this.findParentIdx(idx)]; } findLeftChild(idx) { return this.items[this.findLeftChildIdx(idx)]; } findRightChild(idx) { return this.items[this.findRightChildIdx(idx)]; } size() { return this.items.length; } } class MinHeap extends Heap { bubbleUp() { let index = this.items.length - 1; while (this.findParent(index) && this.findParent(index)[1] > this.items[index][1]) { this.swap(index, this.findParentIdx(index)); index = this.findParentIdx(index); } } bubbleDown() { let index = 0; while ( (this.findLeftChild(index) && this.findLeftChild(index)[1] < this.items[index][1]) || (this.findRightChild(index) && this.findRightChild(index)[1] < this.items[index][1]) ) { let smallerIndex = this.findLeftChildIdx(index); if ( this.findRightChild(index) && this.findRightChild(index)[1] < this.items[smallerIndex][1] ) { smallerIndex = this.findRightChildIdx(index); } this.swap(index, smallerIndex); index = smallerIndex; } } add(value) { this.items.push(value); this.bubbleUp(); } poll() { if (this.size() === 1) { return this.items.pop(); } const value = this.items[0]; this.items[0] = this.items.pop(); this.bubbleDown(); return value; } } function solution(n, paths, gates, summits) { const MAX = 10000001; const answer = [n, MAX]; const hikingTrail = Array.from({ length: n + 1 }, () => []); const isSummits = Array.from({ length: n + 1 }, () => false); summits.sort((a, b) => a - b); summits.forEach((summit)=>{ isSummits[summit] = true; }); paths.forEach((path) => { const [i, j, w] = path; hikingTrail[i].push([j, w]); hikingTrail[j].push([i, w]); }); function dijkstra() { const minHeap = new MinHeap(); const intensity = Array(n + 1).fill(MAX); gates.forEach((gate) => { minHeap.add([gate, 0]); intensity[gate] = 0; }); while (minHeap.size()) { const [vertex, cost] = minHeap.poll(); if (intensity[vertex] < cost) { continue; } if (isSummits[vertex]) { continue; } const adjList = hikingTrail[vertex]; const adjListLen = adjList.length; for (let i = 0; i < adjListLen; i++) { const [nextVertex, nextCost] = adjList[i]; if (intensity[nextVertex] > Math.max(intensity[vertex], nextCost)) { intensity[nextVertex] = Math.max(intensity[vertex], nextCost); minHeap.add([nextVertex, intensity[nextVertex]]); } } } return intensity; } const intensity = dijkstra(); summits.forEach((summit) => { if (intensity[summit] < answer[1]) { answer[0] = summit; answer[1] = intensity[summit]; } }); return answer; }
훔쳐보기스터디원 중 BFS를 한 번 돌려(시작점을 다 넣어주는 것은 다익스트라와 동일) 현재 정점에서 intensity가 작은 정점부터 방문하며 진행했던 코드도 있었다. 다른 스터디원은 다익스트라를 한 번만 돌리는 건 아니었는데도 시간 초과가 발생하지 않았다. 그 스터디원분께 피드백 받았을 때는 동일한 로직으로 JavaScript는 시간 초과가 발생했었는데 원인은 정확히 파악하지 못했다(...😓)
프로그래머스의 다른사람 풀이도 훔쳐봤는데, 내 코드의 경우 MinHeap을 구현하는 코드가 굉장히 길어서 이상하게 눈치(?)가 보였는데 다른 분들도 구현 방식은 다르나 MinHeap을 구현하신 분들도 있었고, BFS로 풀이하신 분들도 있었다.
- 시간 초과가 발생했던 이유
