[프로그래머스] 합승 택시 요금(JavaScript)

🍀 목차
문제
설계
구현(JavaScript)
최종 코드
훔쳐보기

문제

https://programmers.co.kr/learn/courses/30/lessons/72413

코딩테스트 연습 - 합승 택시 요금

 

설계

사실 이 문제를 처음 풀려고 했을 때, 플로이드-워셜 같은데?! 했었는데 플로이드-워셜을 코드를 참고하지 않고 짤 수 없어서 정리했었다. 제대로 정리하니 다행히 다른 참고자료를 보지 않고 풀었다. 😂 하지만 여전히 그래프 문제가 나오면 손에 식은땀부터 난다...

• 왜 플로이드-워셜이라고 생각했나? 
  • 우선 모든 점을 연결하지 않아도 되므로 최단 경로 알고리즘을 써야겠다고 생각했다.
  • 각 정점을 합승하는 경우들을 생각해야 할 것 같아 미리 각 정점의 최단 경로가 계산되어있으면 편할 것 같았다.
  • 다익스트라로도 생각해 봤지만 어떻게 구현해야 할지 설계가 복잡해지기 시작했다. 🌌
  • 지점 개수 n이 최대 200개이므로 200X200X200 = 8,000,000. 플로이드-워셜로도 접근 가능한 문제라고 생각했다.

 

• 해줘야 할 것들
  • dist 배열을 Infinity로 초기화하되, dist[i][j]에서 i===j일 경우는 0으로 초기화해줄 것.
  • 무향 그래프이므로 dist[i][j]와 dist[j][i] 둘 다 요금을 넣어주기.

 

구현(JavaScript)

입출력 예 #1

 

 해당 그래프 정보를 저장할 dist 배열을 만들어준다. 지점수 n 크기의 이차원 배열이다. 

  const dist = Array.from(Array(n),()=>Array(n).fill(Infinity));

 지점 사이의 예상 택시요금을 나타내는 fares 정보를 넣어준다. 내 코드의 경우 dist배열의 인덱스를 1~n이 아닌 0~n-1까지 쓰므로 -1을 해줘야 한다.

  fares.forEach((el)=>{
        const [c,d,f]=el;
        dist[c-1][d-1]=f;
        dist[d-1][c-1]=f;
    }); //연결 정보 저장

 자기 자신으로 가는 경로는 0으로 초기화해준다. Infinity로 해줄 경우 내 코드의 경우에는 입출력 예 #2처럼 출발지점 s를 경유지로 거칠 경우(합승하지 않을 경우)를 계산할 때와 입출력 예 #3처럼 중간에 둘 중에 한 명이 내릴 경우(경유지와 도착지가 같음)를 계산할 때 dist[i][j]에서 i===j가 되며 이상한 값들이 들어가게 된다. 그래서 내 코드에서는 i===j일 때 0으로 만들어주었다.

for(let i=0;i<n;i++){
        dist[i][i]=0;
    }

세팅이 다 된 후

 플로이드-워셜 알고리즘을 사용하여 각 정점과 각 정점 사이의 최소 요금을 계산해준다.

    for(let k=0;k<n;k++){ //경유지
        for(let i=0;i<n;i++){ //출발지
            for(let j=0;j<n;j++){ //도착지
                if(i===j){ //어차피 0이므로 계산할 필요가 없다.
                    continue;
                }
                if(dist[i][k] === Infinity || dist[k][j] === Infinity){
                    continue;
                }                
                dist[i][j] = Math.min(dist[i][j], dist[i][k]+dist[k][j]);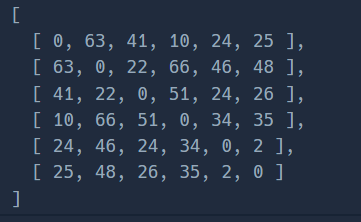             
            }
        }
    }

플로이드-워셜 알고리즘 실행 후

 

 구해진 최소 비용을 토대로 각 정점을 합승 도착지로 생각하며 정답을 구해간다. 

각 정점을 합승 도착지로?
👉 현재 정점까지 '같이'간다고 생각하여 dist[출발지점][현재 정점]+dist[현재 정점][a의 도착지점]+dist[현재 정점][b의 도착지점]을 계산해 주는 것이다. 

 

 처음에 이 부분에서 헷갈려서 2를 나눠줘야 하나, 둘이 같이 합승했는지 어떻게 알지?! 등등 여러 생각을 했었는데 출발지점 s부터 현재 정점까지 a, b가 같이 가는 비용 + 현재 정점에서 a는 자기 갈길 가는 비용 + 현재 정점에서 b는 자기 갈길 가는 비용이라고 생각하면 된다. 이미 dist 배열에는 각 정점과 정점 사이의 최소 택시 요금이 기록되어 있으므로 활용만 하면 된다. 

 let answer = Infinity;

for(let i=0;i<n;i++){
        answer = Math.min(answer, dist[s-1][i]+dist[i][a-1]+dist[i][b-1]);
    }

 위의 그래프 정보로 만들어진 dist로 dist[출발지점][현재 정점]+dist[현재 정점][a의 도착지점]+dist[현재 정점][b의 도착지점]을 계산을 해보면(s=4, a=6, b=2는 다 -1씩 빼주기)

i=0(정점 1까지 합승한다.)	dist[3][0]+dist[0][5]+dist[0][1]	10+25+63 = 98
i=1(정점 2까지 합승한다.)	dist[3][1]+dist[1][5]+dist[1][1]	66+48+0 = 114
i=2(정점 3까지 합승한다.)	dist[3][2]+dist[2][5]+dist[2][1]	51+26+22 = 99
i=3(정점 4까지 합승한다.)	dist[3][3]+dist[3][5]+dist[3][1]	0+35+66 = 101
i=4(정점 5까지 합승한다.)	dist[3][4]+dist[4][5]+dist[4][1]	34+2+46 = 82
i=5(정점 6까지 합승한다.)	dist[3][5]+dist[5][5]+dist[5][1]	35+0+48 = 83

 이렇게 정점 5까지 합승하는 것이 최저 택시요금이 된다.

 

최종 코드

function solution(n, s, a, b, fares) {
    let answer = Infinity;
    const dist = Array.from(Array(n),()=>Array(n).fill(Infinity));

    fares.forEach((el)=>{
        const [c,d,f]=el;
        dist[c-1][d-1]=f;
        dist[d-1][c-1]=f;
    }); //연결 정보 저장

    for(let i=0;i<n;i++){
        dist[i][i]=0;
    }

    for(let k=0;k<n;k++){ //경유지
        for(let i=0;i<n;i++){ //출발지
            for(let j=0;j<n;j++){ //도착지
                if(i===j){
                    continue;
                }
                if(dist[i][k] === Infinity || dist[k][j] === Infinity){
                    continue;
                }                
                dist[i][j] = Math.min(dist[i][j], dist[i][k]+dist[k][j]);             
            }
        }
    }
    
    for(let i=0;i<n;i++){
        answer = Math.min(answer, dist[s-1][i]+dist[i][a-1]+dist[i][b-1]);
    }

    return answer;
}

훔쳐보기

 다익스트라로는 어떤 식으로 구현할까 훔쳐봤다. 출발지점 s에서 a의 도착지점까지의 최단거리 + 출발지점 s에서 b의 도착지점까지의 최단거리를 각각 다익스트라를 활용해 구하고 초기값으로 준 후 s가 아닌 다른 지점까지 합승했을 때 비용과 비교한다. 똑같은 설계지만 플로이드-워셜을 한 번 돌려 dist를 완성시킨 후 돌리냐 와 각 정점끼리의 최단 거리를 다익스트라로 각각 돌리냐의 차이가 있었다.