[프로그래머스] 표현 가능한 이진트리(JavaScript)

🍀 목차
문제
설계
구현(JavaScript)
최종 코드

 

문제

https://school.programmers.co.kr/learn/courses/30/lessons/150367

프로그래머스

 

설계

 

 

(1) 표현 가능한 이진트리 경우의 수(h = 1(최소))

• 루트 노드가 0일때

루트 노드가 0이라면 왼쪽, 오른쪽 자식 노드 모두 0인 "000"만 가능

• • 루트 노드가 1일 때

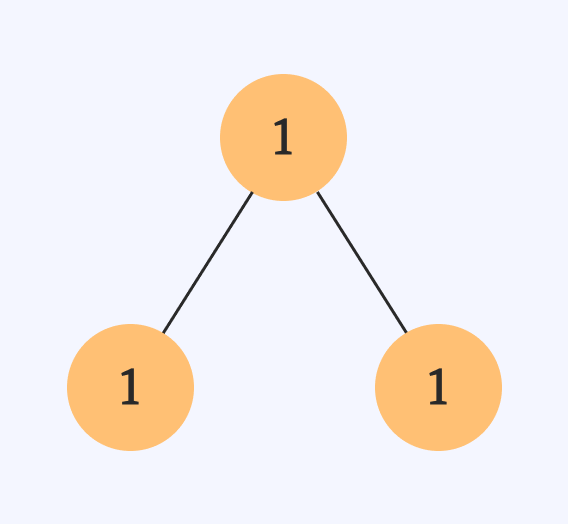
경우의 수 1, "111"

 

경우의 수 2, "110"

 

경우의 수 3, "011"

 

경우의 수 4, "010"

 

(2) 더미 노드를 채워 포화 이진트리로 만드는 부분

• 높이가 h인 포화 이진트리 노드 수는 2^(h+1) - 1라는 것을 이용한다. 
• 문제를 왼쪽 서브 트리, 루트, 오른쪽 서브 트리로 생각할 수 있다(분할 정복). 

구현(JavaScript)

 

1. 입력받은 수를 이진수로 변환한다. 

let binaryString = number.toString(2);

 

 

2. 해당 이진수를 포화 이진트리 형태로 만든다.

 

 

입출력 예시를 보다 보면 포화 이진트리 개수가 될 때까지 앞에 0(더미 노드)을 추가해야 된다는 것을 알 수 있다.

 

 42를 이진수로 변환하면 "101010"인데 이를 노드 7개인 포화 이진트리로 만들려면 앞에 "0" 한 개를 추가해줘야 하고, 그렇게 만들어진 "0101010"으로 입출력 예 #1 42 이진트리가 된 것을 볼 수 있기 때문이다.

 

"0101010"

 

 

변환된 이진수 길이에 따른 결괏값 h를 생각해 보면...  (2^(h+1) - 1)

length(이진수 길이)	h+1	0으로 채워야 할 갯수
1 (ex. "0")	1 (노드 1개의 포화 이진 트리, h = 0)	1(구해진 포화 이진 트리 필요 노드 수) - 1(length) = 0개
2 (ex. "11")	2 (노드 3개의 포화 이진 트리, h = 1)	3 - 2 = 1개 ("0" + "11")
3 (ex. "111")	2	0개 ("111")
4 (ex. "1111")	3 (노드 7개의 포화 이진 트리, h = 2)	7 - 4 = 3개 ("000"+"1111")
5	3	2
8	4(노드 15개의 포화 이진 트리. h = 3)	15 - 8 = 7
9	4	6

 

 

이를 어떻게 표현할 수 있을까?

Math.log2()를 활용하면 된다. 

 

 length에 log2를 취한다면 우리가 찾고 있는 h를 구하는 데 가까워진다. 위의 표를 보면 length가 2의 거듭제곱일 때(볼드체로 강조된 length들) h+1의 값이 변화한다는 것을 알 수 있기 때문이다.

 

 다만 우리가 원하는 값과 조금씩 다르기에...

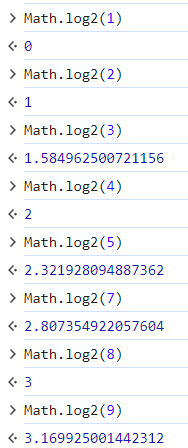
log2를 취한 결과

 

이는 소수점 버림(floor)해주면 된다. 그렇게 구해진 포화 이진트리 노드의 수를 구하는 식은 아래와 같다.

 

const len = binaryString.length;
const perfectBinaryTreeCount = Math.pow(2, Math.floor(Math.log2(len))+1)-1;

 

0으로 채워야 하는 개수 = 포화 이진트리 노드 수 - length이므로

binaryString = "0".repeat(perfectBinaryTreeCount-len) + binaryString;

 

 

3. 만들어진 포화 이진트리 형태를 표현 가능한지 검증한다. 

 

가장 작은 h = 0인 포화 이진트리 "0"과 "1"은 올바른 형태이기에 True를 리턴,

h = 1부터는 루트 노드와 따라 다른 검증을 해야 한다.

설계 단계에서 확인한 표현 가능한 이진트리 경우의 수를 보면 루트 노드가 0일 때는 왼쪽 자식, 오른쪽 자식 노드 모두 0이어야 한다.

이는 다르게 말하면 1이 하나라도 있으면 표현 불가능한 이진트리가 되는 것이다.

 

 루트 노드가 1일 때는 왼쪽 서브 트리가 모두 표현 가능, 오른쪽 서브 트리가 모두 표현 가능하다면 표현 가능한 트리가 된다.

이는 표로 생각해 보면

왼쪽 서브 트리 표현 가능 여부	오른쪽 서브 트리 표현 가능 여부	나와야 할 결괏값
true	true	true
false	true	false
false	false	false

 

인데, 비트 연산 &나 논리곱(&&) 사용하면 둘 중 하나라도 false면 false가 나오게 된다.

이를 이용하여 재귀 형태로 구현해 주면 된다.

 

const isBinaryTree = (str) => {
        if(str.length === 1){
            return true;
        }

        const mid = Math.floor(str.length/2);
        const left = str.slice(0,mid);
        const right = str.slice(mid+1);
        
        if(str[mid] === '0'){
            if(left.includes('1') || right.includes('1')){
                return false;
            }
            return true;
        }

        return isBinaryTree(left) & isBinaryTree(right);
    }

 

최종 코드

function solution(numbers) {
  const answer = [];
  const SUCCESS_NUM = 1,
    FAIL_NUM = 0;

  const isBinaryTree = str => {
    if (str.length === 1) {
      return true;
    }

    const mid = Math.floor(str.length / 2);
    const left = str.slice(0, mid);
    const right = str.slice(mid + 1);

    if (str[mid] === '0') {
      if (left.includes('1') || right.includes('1')) {
        return false;
      }
      return true;
    }

    return isBinaryTree(left) & isBinaryTree(right);
  };

  numbers.forEach(number => {
    let binaryString = number.toString(2);
    const len = binaryString.length;
    const perfectBinaryTreeCount =
      Math.pow(2, Math.floor(Math.log2(len)) + 1) - 1;

    binaryString = '0'.repeat(perfectBinaryTreeCount - len) + binaryString;

    const result = isBinaryTree(binaryString);
    if (result) {
      answer.push(SUCCESS_NUM);
    }
    if (!result) {
      answer.push(FAIL_NUM);
    }
  });

  return answer;
}